CALCULO INTEGRAL Y ECUACIONES DIFERENCIALES
INDICE
ECUACIONES DIFERENCIALES
4.1 Teoria preliminar
4.1.1 Sistema de ecuaciones diferenciales lineales
4.1.2 Sistema de ecuaciones diferenciales lineales homogeneas
4.1.3Solucion general y particular de EDL
4.2Metodos de solucion de EDL
4.2.1Metodos de los operadores
4.2.3utilidad TL
4.3Aplicaciones
CALCULO INTEGRAL
3.1 Áreas
3.1.1 Áreas bajo la grafica de una función
3.1.2 área entre la grafica de las funciones
3.2 longitud de curvas
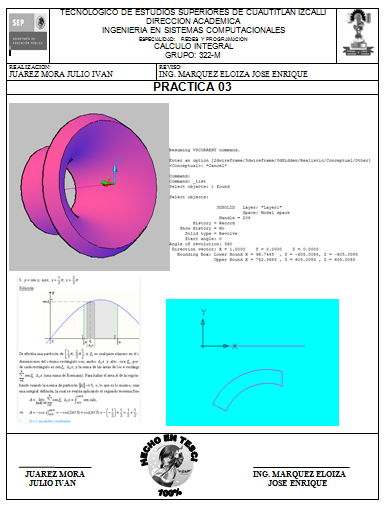
3.3 Calculo de volúmenes sólidos de revolución
3.4 Calculo de centroides
3.5 Otras aplicaciones
4.1 Definición de serie
4.1.1 Finita
4.1.2 Infinita (criterio de D´Alembert)
4.2 Serie numérica convergencia
4.3 Serie de potencias
4.4 Radio de convergencia
4.5 Serie de Taylor
4.6 Representación de funciones por serie de Taylor
4.7 Cálculo de integrales expresadas como serie de Taylor
martes, 26 de junio de 2012
4.2 Metodos de solucion para sistemas de ED
Transformada Integral
Si f(x,y) es una funcion de dos variables, entonces una integral definida de f con respecto a una de las variables lleva a una funcion de la otra variable. Por ejemplo, si se mantiene y constante. De manera similar,
una integral definida tranforma una funcion f de la variable t en una funcion F de la variable s. Se tiene interes
particular en una transformada integral, donde el intervalo de integracion es el intervalo no acotado.
4.1 Teorema Preliminar
4.1.1 Sistemas de EDL
4.1.2 Sistemas de EDL homogeneas
4.1.3 Solucion general y solucion particular de EDL
Las ecuaciones diferenciales ordinarias simultaneas comprenden dos o mas ecuaciones
que contienen las derivadas de dos o mas funciones incognitas de una sola variable
independiente.
Solucion de un sistema
Una solucion de un sistema de ecuaciones diferenciales es un conjunto de funciones diferenciales
x=f(t), y(t), z = h(t),etc., que satisfacen cada ecuacion del sistema en algun intervalo I.
4.1.2 Sistemas de EDL homogeneas
4.1.3 Solucion general y solucion particular de EDL
Las ecuaciones diferenciales ordinarias simultaneas comprenden dos o mas ecuaciones
que contienen las derivadas de dos o mas funciones incognitas de una sola variable
independiente.
Solucion de un sistema
Una solucion de un sistema de ecuaciones diferenciales es un conjunto de funciones diferenciales
x=f(t), y(t), z = h(t),etc., que satisfacen cada ecuacion del sistema en algun intervalo I.
miércoles, 13 de junio de 2012
4.3 APLICACIONES
Nuestro objetivo será resolver dicho sistema de ecuaciones diferenciales lineales. Empezaremos por estudiar el sistema homogéneo asociado:
Para después hallar una solución particular del sistema, y tener así la solución general
EJEMPLOS
Sea el sistema de ecuaciones diferenciales lineales:
Evidentemente:
Hallamos la solución general del sistema de ecuaciones diferenciales homogéneo asociado al sistema dado:
Su polinomio característico es:
Sus autovalores son:
Estudiamos el autovalor :
Eso implica que el autoespacio asociado tiene dimensión 1, con lo que le corresponde una única caja. Por tanto la matriz de Jordán correspondiente será:
Luego la forma real de Jordán será:
La base asociada a es:
Operando con ella:
La base asociada a es:
Por tanto la base asociada a es:
Luego la base total será:
Y pasando a la forma real de la base de Jordán:
Por tanto la matriz de paso será:
Resolvemos:
Y ahora hallamos la solución particular:
viernes, 1 de julio de 2011
3.1 areas
Área de una función y el eje de abcisas 15.2
Cálculo de áreas




3 Calcula el área del recinto limitado por la parábola f(x) = x2 y las rectas y = 0, x = 1, x = 3.
 |  |
lunes, 27 de junio de 2011
3.2 Longitud de curvas
Longitud de curvas planas


La longitud de una curva plana se puede aproximar al sumar pequeños segmentos de recta que se ajusten a la curva, esta aproximación será más ajustada entre más segmentos sean y a la vez sean lo más pequeño posible.
Definición:
Si la primera derivada de una función es continua en [a,b] se dice que es suave y su gráfica es una curva suave.

Cuando la curva es suave, la longitud de cada pequeño segmentos de recta se puede calcular mediante el teorema de Pitágoras y (dL)2=(dx)2+(dy)2, de tal forma que sumando todos los diferenciales resulta:
Definición:
Si f es suave en [a,b], la longitud de la curva de f(x) desde a hasta b es:

EJEMPLOS: AQUI
Ejercicios Calcule la longitud de las siguientes curvas: Parámetricasa) b)La astroide c)  Calcule la longitud del segmento de curva desde a) b) |
3.4 CALCULO DE CENTROIDES
El centroide, centro geométrico o baricentro de una figura plana o tridimensional forma dos X es la intersección de todas las líneas rectas que dividen a X en dos partes de igual momento sobre la línea. Informalmente, es el “promedio” (media aritmética) de todos los puntos de X. La definición se extiende a todo objeto X de n - dimensiones del espacio: su centro de gravedad es la intersección de todos los hiperplanos que dividen a X en dos partes de igual momento.
En la física, la palabra centroide significa que el centro geométrico del objeto de la forma, como antes, pero baricentro también puede significar su físico centro de la masa o el centro de gravedad, según el contexto. Informalmente, el centro de la masa (y centro de gravedad en un campo gravitatorio uniforme) es el promedio de todos los puntos, ponderado por el local de la densidad o peso específico. Si un objeto físico tiene uniforme de densidad, entonces su centro de masa es el mismo que el centro de gravedad de su forma.
En geografía, el centro de gravedad de una región de la superficie de la Tierra, proyectada radialmente sobre dicha superficie, se conoce como su centro geográfico.
Propiedades
El centroide geométrico de un objeto convexo siempre se encuentra en el objeto. Un objeto A-convexa no puede tener un centro de gravedad que está fuera de la propia figura. El centro de gravedad de un anillo o un tazón de fuente, por ejemplo, se encuentra en la central de vacío del objeto.
Suscribirse a:
Entradas (Atom)