3.1 areas

Área de una función y el eje de abcisas                  15.2

Cálculo de áreas

3  Calcula el área del recinto limitado por la parábola f(x) = x² y las rectas y = 0, x = 1, x = 3.

3.2 Longitud de curvas

Longitud de curvas planas

La longitud de una curva plana se puede aproximar al sumar pequeños segmentos de recta que se ajusten a la curva, esta aproximación será más ajustada entre más segmentos sean y a la vez sean lo más pequeño posible.

Definición:

Si la primera derivada de una función es continua en [a,b] se dice que es suave y su gráfica es una curva suave.

Cuando la curva es suave, la longitud de cada pequeño segmentos de recta se puede calcular mediante el teorema de Pitágoras y (dL)²=(dx)²+(dy)², de tal forma que sumando todos los diferenciales resulta:

Definición:

Si f es suave en [a,b], la longitud de la curva de f(x) desde a hasta b es:

EJEMPLOS:  AQUI

Ejercicios Calcule la longitud de las siguientes curvas: Parámetricas a)   b)La astroide con  c)   Calcule la longitud del segmento de curva desde  hasta a)   b)

3.3 Calculo de volúmenes sólidos de revolución

3.4 CALCULO DE CENTROIDES

El centroide, centro geométrico o baricentro de una figura plana o tridimensional forma dos X es la intersección de todas las líneas rectas que dividen a X en dos partes de igual momento sobre la línea. Informalmente, es el “promedio” (media aritmética) de todos los puntos de X. La definición se extiende a todo objeto X de n - dimensiones del espacio: su centro de gravedad es la intersección de todos los hiperplanos que dividen a X en dos partes de igual momento.

En la física, la palabra centroide significa que el centro geométrico del objeto de la forma, como antes, pero baricentro también puede significar su físico centro de la masa o el centro de gravedad, según el contexto. Informalmente, el centro de la masa (y centro de gravedad en un campo gravitatorio uniforme) es el promedio de todos los puntos, ponderado por el local de la densidad o peso específico. Si un objeto físico tiene uniforme de densidad, entonces su centro de masa es el mismo que el centro de gravedad de su forma.

En geografía, el centro de gravedad de una región de la superficie de la Tierra, proyectada radialmente sobre dicha superficie, se conoce como su centro geográfico.

Propiedades

El centroide geométrico de un objeto convexo siempre se encuentra en el objeto. Un objeto A-convexa no puede tener un centro de gravedad que está fuera de la propia figura. El centro de gravedad de un anillo o un tazón de fuente, por ejemplo, se encuentra en la central de vacío del objeto.

3.5 Otras aplicaciones

OTRAS APLICACIONES


El momento de inercia


El momento de inercia (símbolo I) es una medida de la inercia rotacional de un cuerpo. Cuando un cuerpo gira en torno a uno de los ejes principales de inercia, la inercia rotacional puede ser representada como una magnitud escalar llamada momento de inercia. Sin embargo, en el caso más general posible la inercia rotacional debe representarse por medio de un conjunto de momentos de inercia y componentes que forman el llamado tensor de inercia. La descripción tensorial es necesaria para el análisis de sistemas complejos, como por ejemplo en movimiento de giroscopios.

Dado un sistema de partículas y un eje arbitrario, el momento de inercia del mismo se define como la suma de los productos de las masas de las partículas por el cuadrado de la distancia r de cada partícula a dicho eje. Matemáticamente se expresa como:

Para un cuerpo de masa continua (Medio continuo), se generaliza como:

El subíndice V de la integral indica que se integra sobre todo el volumen del cuerpo. Se resuelve a través de una integral triple.

Fuente:http://www.itescam.edu.mx/principal/webalumnos/sylabus/asignatura.php?clave_asig=ACF-0902&carrera=ISIC-2010-224&id_d=133

4.1 Definición de serie

En matemáticas, una serie es la suma de los términos de una sucesión. Se representa una serie con términos a_n como donde n es el índice final de la serie. Las series infinitas son aquellas donde i toma el valor de absolutamente todos los números naturales, es decir, .

Las series convergen o divergen. En cálculo, una serie diverge si no existe o si tiende a infinito; puede converger si para algún .

• Una serie geométrica es una serie en la cual cada término se obtiene multiplicando el anterior por una constante, llamada razón. Ejemplo (con constante 1/2):

En general, una serie geométrica, de razón z, es convergente, sólo si |z| < 1, a:

• La serie armónica es la serie

La serie armónica es divergente.

• Una serie alternada es una serie donde los términos alternan el signo. Ejemplo:

• Una serie telescópica es la suma , donde a_n = b_n − b_n+1. Se representa de la siguiente manera:

La convergencia de dicha serie y su suma se pueden calcular fácilmente, ya que:

• Una serie hipergeométrica^[1] es una serie de la forma , que cumple que = .

4.1.1 Finita

Una serie es la suma de los términos de una sucesión. Se representa una serie con términos a_n como  

donde n es el índice final de la

serie. Las series infinitas son aquellas donde i toma el valor de absolutamente todos los números naturales, es decir,      .

Las series convergen o divergen. En cálculo, una   serie diverge si    no existe o si tiende a infinito; puede converger si 

Serie finita

x_i = 0 para todo i > n y y_i = 0 para todo i > m. En este caso el producto de

Cauchy de   

Por lo tanto, para series finitas (que son sumas finitas), la multiplicación de Cauchy es directamente la multiplicación de las series.

Serie infinita

§  Primer ejemplo. Para alguna      

                 por definición y la fórmula binomial. Dado que, formalmente    se ha demostrado que   

Como el límite del producto de Cauchy de dos series absolutamente convergentes es igual al producto de los límites de esas series (véase debajo), se ha demostrado por lo tanto la fórmula exp(a + b) = exp(a)exp(b) para todo   

Segundo ejemplo. Sea x(n) = 1 para todo, por lo tanto el producto de Cauchy

                               fuente: http://es.wikipedia.org/wiki/Serie_matem%C3%A1tica 

4.2 Serie numérica convergencia

SERIES NUMERICAS.

1. Convergencia.

Si {an} es una sucesi´on de numeros reales, se define la serie de termino general an y

se escribe

P1

n=1 an como:

1X

n=1

an = lim (a1 + · · · + an).

Si este l´ımite de la n-´esima suma parcial a1 + · · · + an es finito, se dice que la serie es

convergente; si es infinito o no existe, que es divergente.

2. Convergencia absoluta.

Se dice que la serie

P

an es absolutamente convergente si la serie

P

|an| es convergente.

Toda serie absolutamente convergente es convergente.

Si una serie es absolutamente convergente, entonces cualquier reordenaci´on suya tambi

´en lo es y tiene el mismo valor.

Se dice que una serie es condicionalmente convergente si es convergente, pero no

absolutamente convergente.

3. Propiedades.

• El car´acter (convergente o divergente) de una serie no cambia si se modifica un

n´umero finito de sus terminos.

• Para que la serie

P

an converja es necesario que lim an = 0.

• Si las series Pan y Pbn convergen, entonces: Pan + bn y P_an, con _ 2 R,

tambien, teniendose:

X

(an + bn) Xan +Xbn yX_an = _Xan.

4.3 Serie de potencias

Serie de potencias

Es una serie de ecuaciones que tiene la forma

a0 + a1 (x-a) + a2  (a-x)^2 + ……… an (x-a)^n + ……….

A esto se le llama serie de potencias, aquí las constantes a0, a1…….., an……., se llaman también los coeficientes de la serie. Esta serie está dispuesta según las potencias crecientes del binomio x-a.

Cuando a=0, tenemos una serie de potencias de x que es un caso particular de la serie.

Para determinar el dominio de convergencia de la serie sustituimos en esta ecuación la variable

x – a =X

Después de la sustitución la ecuación toma el siguiente aspecto:

a0 + a1X + a2X^2 +………+ anX^n +…….,

Es decir hemos obtenido la serie de potencias de X. 

4.4 Radio de convergencia

En matemáticas, según el teorema de Cauchy-Hadamard, el radio de convergencia de una serie de la forma , con , viene dado por la expresión:

DEFINICION


Si nos limitamos al conjunto de los números reales, una serie de la forma , con , recibe el nombre de serie de potencias centrada en x₀. La serie converge absolutamente para un conjunto de valores de x que verifica que | x − x₀ | < r, donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de x pertenecientes al intervalo (x₀ − r, x₀ + r), ya que la convergencia para los extremos de este ha de estudiarse aparte, por lo que el intervalo real de convergencia puede ser también semiabierto o cerrado. Si la serie converge solo para x₀, r = 0. Si lo hace para cualquier valor de x, r = 













EJEMPLOS

Mostraremos el radio de convergencia de algunos desarrollos en series de potencias con sus respectivos radios de convergencia sin justificar porqué el radio de convergencia es el dado.

Radio de convergencia finito

La función 1 / (1 − x) en su desarrollo con centro 0, o sea, en series de potencia x − x₀ = x − 0 = x, tiene el siguiente aspecto:

.

(para el cálculo de la serie vea serie de Taylor). Su radio de convergencia es r = 1. Eso significa que para calcular si tomo cualquier valor cuya distancia al x₀ = 0 es menor que r = 1, por ejemplo el x = 0.25, entonces al remplazarlo en la serie el resultado de calcular la serie será el mismo que remplazarlo en la función, de hecho

.

(la cuenta se puede hacer por serie de potencia). Y por otro lado

.

Pero si tomamos un elemento fuera del radio de convergencia, por ejemplo el x = 2, los más probable es que al remplazarlo en la serie, ésta diverja (por eso el nombre de radio de convergencia). Efectivamente:

.

Distancia a la singularidad

El cálculo del radio de convergencia no es simple. Veamos una función con dos desarrollos en serie con distintos centros y analicemos sus radios de convergencia. La misma función 1 / (1 − x) en su desarrollo con centro x₀ = 3 tiene la forma:

.

Pero en este caso su radio de convergencia es r = 2. Notemos que la función 1 / (1 − x) tiene una singularidad en el 1; y que en los dos caso anteriores el radio de convergencia coincide con la distancia del centro a la singularidad: | 0 − 1 | = 1 y | 3 − 1 | = 2. Esto será siempre verdadero para ésta función, pero, no puede generalizarse, como veremos en el siguiente ejemplo:

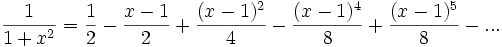
Como no hay singularidades reales podría suponerse que el radio es infinito, sin embargo su radio de convergencia es . Este radio parece caprichoso pero tiene que ver con el hecho de que pasando la función a dominio complejo, existe una singularidad en el denominador.La serie

Radio de convergencia infinito

Por ejempo, la función e^x puede desarrollarse en series de potencia de x − 0 = x, de hecho .

y esto vale para todo real x por eso el radio de convergencia será infinito.